某公司利用两种原料 A、B生产甲 、乙两种产品 , 各产品所需的原料数 、原料限量及单位产品所获利润如题表。企业目标是追求利润的最大化 ,试写出该线性规划问题的数学模型 ,并用图解法求出最优解和最大利润。
【正确答案】：
设生产甲产品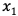
吨，乙产品
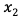吨，线性规划模型如下：
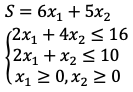
求S的最大值。
最优解是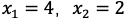
，最大利润是MAXS=34（万元）。
【题目解析】：
第一步：建立模型。
（1）目标函数：总利润最大，即求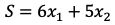
的最大值。
（2）约束条件：
原料A不多于16吨，原料B不多于10吨，可得：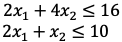
变量非负条件：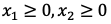
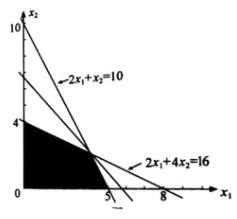
第二步：图解法求最优解。
根据约束条件求得目标函数的可行解区，根据线性规划的基本原理，最优解必然出现在可行解区边缘折线的凸交点上，通过计算得，目标函数在点（4，2）处取最大值，求得最大利润为6×4+5×2=34（万元）。