设有字符集{A,B,C,D,E,F},各字符使用频率对应为{2, 4, 5, 13, 9, 18}。
试画出哈夫曼树(要求任一结点的左孩子权值小于右孩子)。
【正确答案】:
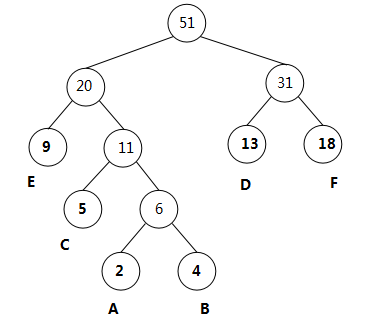
【题目解析】:
哈夫曼算法非形式的描述如下:
(1)由给定的值{2, 4, 5, 13, 9, 18}构造森林F= {2, 4, 5, 13, 9, 18},其中每个树为一棵只有根结点且其权为给定值的二叉树。
(2)从F中选取根结点的权最小的两棵二叉树2和4,构造一棵分别以2和4为左、右子树的新的二叉树,且置该二叉树的根结点的权2+4=6。
(3)从F中删去2、4,并将6加入F。此时F= {6, 5, 13, 9, 18}。此时F中仍多于一棵二叉树,则返回(2),F的变化过程为{11, 13, 9, 18},{20, 13, 18},{20, 31},{51}。直到F中只含一棵二叉树为止,这棵二叉树就是哈夫曼树。
且题目要求新二叉树的左子树根的权值小于等于右子树根的权值,故得出如图答案。
