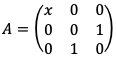与
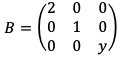相似，求可逆矩阵P使得
【正确答案】：
由于A与B相似，B是对角矩阵，故A的特征值也是2，1，-1，
当
时，方程组(2E-A)X=0的基础解系为
。
当
时，方程组(E-A)X=0的基础解系为
。
当
时，方程组(-E-A)X=0的基础解系为
。
令
，
线性无关，则P可逆且满足。
【题目解析】：A与B相似，B是对角矩阵，故本题实际是求使A相似于B的可逆矩阵P。n阶方阵A相似于对角矩阵⟺对每一个r重特征值λ，均存在r个线性无关的特征向量。（1）遇到矩阵相似对角化的问题，不由分说先求特征值，因相似矩阵必然有相同的特征值，故A的特征值也是2，1，-1。（2）求出每个特征值对应的基础解系，3个基础解系线性无关，故A可以对角化，那么三个基础解系拼成的矩阵即为P。