设3元线性方程组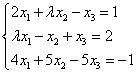
,（1）确定当λ取何值时，方程组有惟一解、无解、有无穷多解？（2）当方程组有无穷多解时，求出该方程组的通解（要求用其一个特解和导出组的基础解系表示）
【正确答案】：
取系数行列式 D＝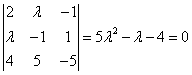
，解得
，
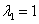，根据克莱默法则，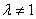
且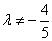
时，方程组有惟一解；当
＝1时，方程组的增广阵为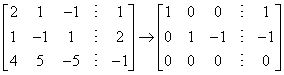 
此时，方程组有无穷多解，其通解为 x＝
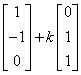，其中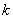
为任意常数；当
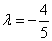时，方程组的增广矩阵为 
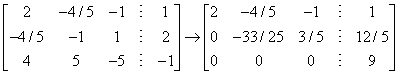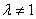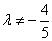此时，方程组无解。总之，（1）当且时，即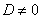
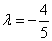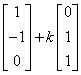，方程组有惟一解，当＝1时，方程组一无穷多解，当时，方程组无解；（2）当＝1时，方程组的通解为x＝，其中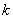为任意常数。