求正交变换x=py,将二次型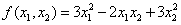 化为标准形,并指出是否为正定二次型.
化为标准形,并指出是否为正定二次型.
【正确答案】:
正交变换方阵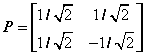 ,使得
,使得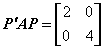 ,它是正定的.
,它是正定的.
【题目解析】:
本题考查正定矩阵.由已知条件得二次型的实对称方阵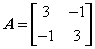 其特征方程为
其特征方程为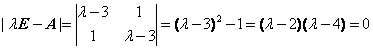 得特征值
得特征值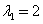 ,
,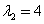 ,当
,当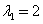 时,解方程组
时,解方程组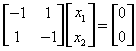 ,得
,得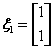 ,单位化为
,单位化为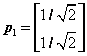 ,当
,当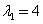 时,解方程组
时,解方程组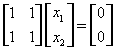 ,得
,得 ,单位化为
,单位化为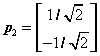 ,所以得正交变换方阵
,所以得正交变换方阵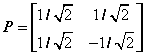 使得
使得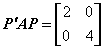 ,正交变换为正交变换为x=py 或
,正交变换为正交变换为x=py 或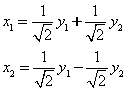 .由于此二次型的特征值均为正数,所以它是正定的. 参见教材P172. (2013年4月真题)
.由于此二次型的特征值均为正数,所以它是正定的. 参见教材P172. (2013年4月真题)
求正交变换x=py,将二次型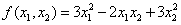 化为标准形,并指出是否为正定二次型.
化为标准形,并指出是否为正定二次型.
求正交变换x=py,将二次型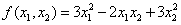 化为标准形,并指出是否为正定二次型.
化为标准形,并指出是否为正定二次型.
正交变换方阵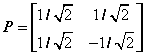 ,使得
,使得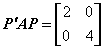 ,它是正定的.
,它是正定的.
本题考查正定矩阵.由已知条件得二次型的实对称方阵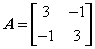 其特征方程为
其特征方程为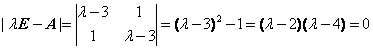 得特征值
得特征值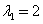 ,
,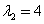 ,当
,当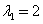 时,解方程组
时,解方程组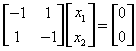 ,得
,得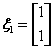 ,单位化为
,单位化为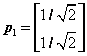 ,当
,当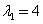 时,解方程组
时,解方程组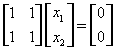 ,得
,得 ,单位化为
,单位化为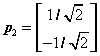 ,所以得正交变换方阵
,所以得正交变换方阵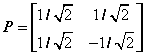 使得
使得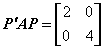 ,正交变换为正交变换为x=py 或
,正交变换为正交变换为x=py 或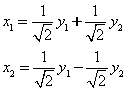 .由于此二次型的特征值均为正数,所以它是正定的. 参见教材P172. (2013年4月真题)
.由于此二次型的特征值均为正数,所以它是正定的. 参见教材P172. (2013年4月真题)