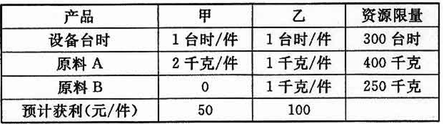
某企业计划期内要安排甲、乙两种产品生产,有关资源消耗及可获利润如下表。该厂要获得利润最大化,应如何安排两种产品的生产?
要求建立该问题的线性规划数学模型并用图解法求出最优解。
【正确答案】:



【题目解析】:
根据约束条件求得目标函数的可行解区,根据线性规划的基本原理,最优解必然出现在可行解区边缘折线的凸交点上,通过计算得,目标函数在点(50,250)处取最大值,求得最大利润为50×50+100×250=27500元。
要求建立该问题的线性规划数学模型并用图解法求出最优解。
">要求建立该问题的线性规划数学模型并用图解法求出最优解。
">某企业计划期内要安排甲、乙两种产品生产,有关资源消耗及可获利润如下表。该厂要获得利润最大化,应如何安排两种产品的生产?

要求建立该问题的线性规划数学模型并用图解法求出最优解。
某企业计划期内要安排甲、乙两种产品生产,有关资源消耗及可获利润如下表。该厂要获得利润最大化,应如何安排两种产品的生产?

要求建立该问题的线性规划数学模型并用图解法求出最优解。



根据约束条件求得目标函数的可行解区,根据线性规划的基本原理,最优解必然出现在可行解区边缘折线的凸交点上,通过计算得,目标函数在点(50,250)处取最大值,求得最大利润为50×50+100×250=27500元。