设f (x)在[0,1]上连续,且当x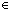 [0,1]时,恒有f (x)<1。证明方程
[0,1]时,恒有f (x)<1。证明方程 在(0,1)内至少存在一个根。
在(0,1)内至少存在一个根。
【正确答案】:
令 则由f (x)在[0,1]上连续,得
则由f (x)在[0,1]上连续,得 在[0,1]上连续,可导又因为
在[0,1]上连续,可导又因为 又由f (x)<1,x
又由f (x)<1,x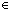 [0,1],∴
[0,1],∴ ∴
∴ 所以由零点定理在
所以由零点定理在 至少有一点
至少有一点 即
即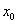 为方程
为方程 的根。
的根。
设f (x)在[0,1]上连续,且当x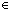 [0,1]时,恒有f (x)<1。证明方程
[0,1]时,恒有f (x)<1。证明方程
设f (x)在[0,1]上连续,且当x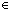 [0,1]时,恒有f (x)<1。证明方程
[0,1]时,恒有f (x)<1。证明方程 在(0,1)内至少存在一个根。
在(0,1)内至少存在一个根。
令 则由f (x)在[0,1]上连续,得
则由f (x)在[0,1]上连续,得 在[0,1]上连续,可导又因为
在[0,1]上连续,可导又因为 又由f (x)<1,x
又由f (x)<1,x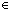 [0,1],∴
[0,1],∴ ∴
∴ 所以由零点定理在
所以由零点定理在 至少有一点
至少有一点 即
即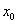 为方程
为方程 的根。
的根。